Regularization
Contents
Regularization¶
This is a supplement material for the Machine Learning Simplified book. It sheds light on Python implementations of the topics discussed while all detailed explanations can be found in the book.
I also assume you know Python syntax and how it works. If you don’t, I highly recommend you to take a break and get introduced to the language before going forward with my code.
This material can be downloaded as a Jupyter notebook (Download button in the upper-right corner ->
.ipynb) to reproduce the code and play around with it.
1. Required Libraries & Data¶
# Import function to automatically create polynomial features!
from sklearn.preprocessing import PolynomialFeatures
# Import Linear Regression and a regularized regression function
from sklearn.linear_model import LinearRegression, Lasso
from sklearn.linear_model import LassoCV
# Finally, import function to make a machine learning pipeline
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import Ridge
import numpy as np
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina' # sharper plots
# Defined data
X_train = [30, 46, 60, 65, 77, 95]
y_train = [31, 30, 80, 49, 70, 118]
X_test = [17, 40, 55, 57, 70, 85]
y_test = [19, 50, 60, 32, 90, 110]
2. Ridge Regression¶
import pandas as pd
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.preprocessing import PolynomialFeatures, scale
#Confusingly, the lambda term can be configured via the “alpha” argument when defining the class. The default value is 1.0 or a full penalty.
degree_=4
lambda_=0.5
# scale the X data to prevent numerical errors.
X_train = np.array(X_train).reshape(-1, 1)
polyX = PolynomialFeatures(degree=degree_).fit_transform(X_train)
model1 = LinearRegression().fit(polyX, y_train)
model2 = Ridge(alpha=lambda_).fit(polyX, y_train)
# print("OLS Coefs: " + str(model1.coef_[0]))
# print("Ridge Coefs: " + str(model2.coef_[0]))
print(f"Linear Coefs: {sum(model1.coef_)}")
print(f"Ridge Coefs: {sum(model2.coef_)}")
Linear Coefs: -64.66185222664129
Ridge Coefs: -7.221838297484756
/Users/andrewwolf/Library/Caches/pypoetry/virtualenvs/themlsbook-8peXrHpY-py3.9/lib/python3.9/site-packages/sklearn/linear_model/_ridge.py:157: LinAlgWarning: Ill-conditioned matrix (rcond=1.10221e-16): result may not be accurate.
return linalg.solve(A, Xy, sym_pos=True, overwrite_a=True).T
t_ = np.array(np.linspace(0, 120, 120)).reshape(-1, 1)
t = PolynomialFeatures(degree=degree_).fit_transform(t_)
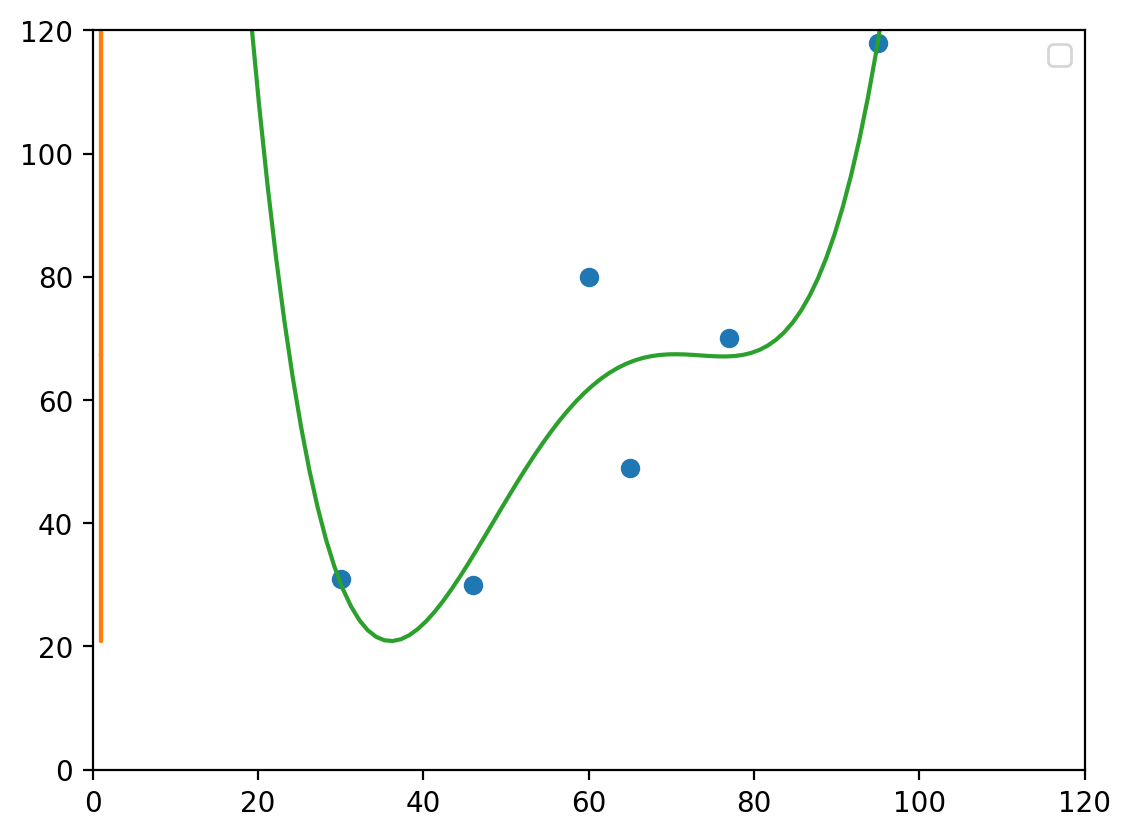
# visualize
plt.plot(X_train, y_train, 'o', t, model2.predict(t), '-')
# plt.scatter(X_train, y_train, color='blue', label='Training set')
# plt.scatter(X_test, y_test, color='red', label='Test set')
plt.legend(loc='best')
plt.ylim((0,120))
plt.xlim((0,120))
plt.show()
No artists with labels found to put in legend. Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
3. Lasso Regression¶
import pandas as pd
from sklearn.linear_model import Lasso, LinearRegression
from sklearn.preprocessing import PolynomialFeatures, scale
#Confusingly, the lambda term can be configured via the “alpha” argument when defining the class. The default value is 1.0 or a full penalty.
degree_=4
lambda_=0
# scale the X data to prevent numerical errors.
X_train = np.array(X_train).reshape(-1, 1)
# y_train = np.array(y_train).reshape(-1, 1)
polyX = PolynomialFeatures(degree=degree_).fit_transform(X_train)
model1 = LinearRegression().fit(polyX, y_train)
model2 = Lasso(alpha=lambda_, max_iter=1300000).fit(polyX, y_train)
print(f"Linear Coefs: {model1.coef_}")
print(f"Lasso Coefs: {model2.coef_}")
/var/folders/5y/7zvhsc3x5nx162713kvx9c1m0000gn/T/ipykernel_73441/4278195487.py:18: UserWarning: With alpha=0, this algorithm does not converge well. You are advised to use the LinearRegression estimator
model2 = Lasso(alpha=lambda_, max_iter=1300000).fit(polyX, y_train)
/Users/andrewwolf/Library/Caches/pypoetry/virtualenvs/themlsbook-8peXrHpY-py3.9/lib/python3.9/site-packages/sklearn/linear_model/_coordinate_descent.py:647: UserWarning: Coordinate descent with no regularization may lead to unexpected results and is discouraged.
model = cd_fast.enet_coordinate_descent(
Linear Coefs: [ 0.00000000e+00 -6.64626506e+01 1.82147242e+00 -2.07589752e-02
8.48966900e-05]
Lasso Coefs: [ 0.00000000e+00 -5.77567467e+01 1.58872837e+00 -1.81456434e-02
7.44216108e-05]
/Users/andrewwolf/Library/Caches/pypoetry/virtualenvs/themlsbook-8peXrHpY-py3.9/lib/python3.9/site-packages/sklearn/linear_model/_coordinate_descent.py:647: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations, check the scale of the features or consider increasing regularisation. Duality gap: 3.281e+02, tolerance: 5.672e-01 Linear regression models with null weight for the l1 regularization term are more efficiently fitted using one of the solvers implemented in sklearn.linear_model.Ridge/RidgeCV instead.
model = cd_fast.enet_coordinate_descent(
sum(model2.coef_)
-56.186089506337865
t_ = np.array(np.linspace(0, 120, 120)).reshape(-1, 1)
t = PolynomialFeatures(degree=degree_).fit_transform(t_)
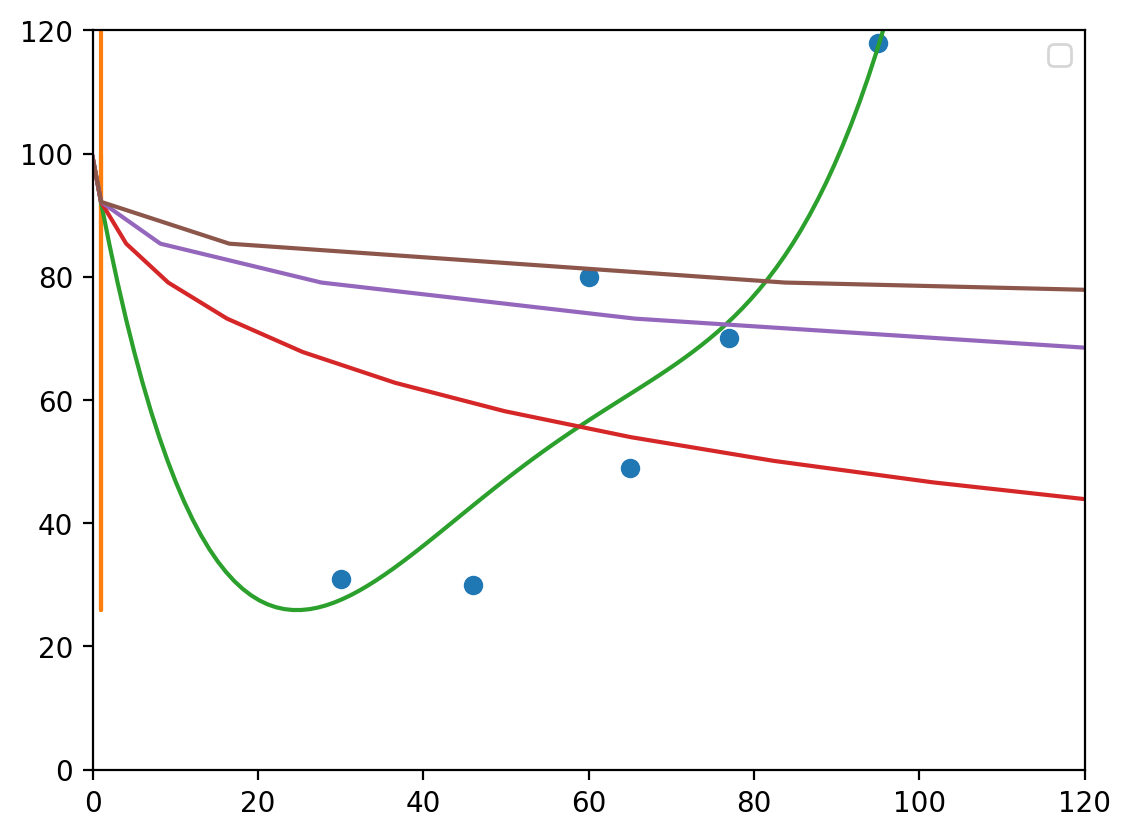
# visualize
plt.plot(X_train, y_train, 'o', t, model2.predict(t), '-')
# plt.scatter(X_train, y_train, color='blue', label='Training set')
# plt.scatter(X_test, y_test, color='red', label='Test set')
plt.legend(loc='best')
plt.ylim((0,120))
plt.xlim((0,120))
plt.show()
No artists with labels found to put in legend. Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
